풀스택을 꿈꾸며

내 이야기를 들어주고 공감해 준다는 것이 큰 힘이 된다는 당연한 사실을 느끼는 한주였네요.. 누군가 나에게 이야기를 한다면 공감을 해주는 그런 사람이 되었으면 좋겠습니다..

2차원 데이타를 1차원으로 가공하여 데이타를 이용하는 것이 낯설었네요... 쉬운 데이타를 이용해서  책에 나온 비지도 학습의 k-means를 따라해봤어요.. 소스와 데이타 파일은 첨부해요..

numpy에서도 axis가 있네요.. pandas와 동일하네요... 정리하면서 왜 이리 깔끔하지 못해 투덜거렸는데... 원죄는 numpy일까???

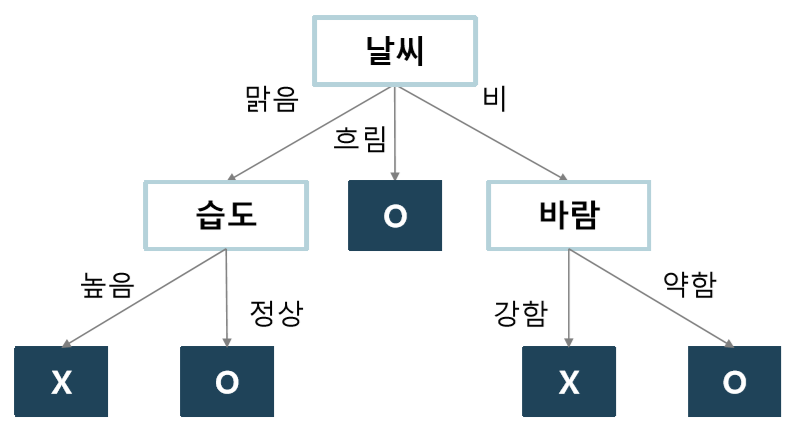
군집화(Clustering)

답/라벨없는 데이터 내에서 거리가 가까운 것들끼리 각 군집들로 분류하는 것이다 (분류라고 표현했지만, 지도학습인 classification과는 다르다). 즉 데이터 내에 숨어있는 패턴, 그룹을 파악하여 서로 묶는 것이라고 할 수 있다. 만약 라벨값이 존재하는 데이터라고 하더라도, 같은 라벨 내에서도 얼마든지 다른 군집으로 묶일 가능성이 있다.

Clustering(군집화) : 비슷한 샘플끼리 그룹으로 모으는 작업

Cluster(클러스터)  : 군집 알고리즘에 의해 만든 그룹

1 K-Means / K-평균

K-Means 클러스터링은 클러스터링에서 가장 일반적으로 사용되는 알고리즘으로, 군집 중심점(centroid)이라는 특정한 임의의 지점을 선택해 해당 중심에 가장 가까운 포인트들을 선택하는 군집화 기법이다. K-Means이므로 K개의 centroid를 지정한다. 이때 가장 가까운 포인트를 선택한다는 점에서 K-Means는 거리 기반 군집화 방법임을 알 수 있다

1. 무작위로 k개의 클러스터 중심을 정한다.
2. 각 샘플에서 가장 가까운 클러스터 중심을 찾아 해당 클러스터의 샘플로 지정한다
3. 클러스터에 속한 샘플의 평균값으로 클러스터 중심을 변경한다.
4. 클러스터 중심에 변화가 없을 때까지 2번으로 돌아가 반복한다.

2 K-평균 실습

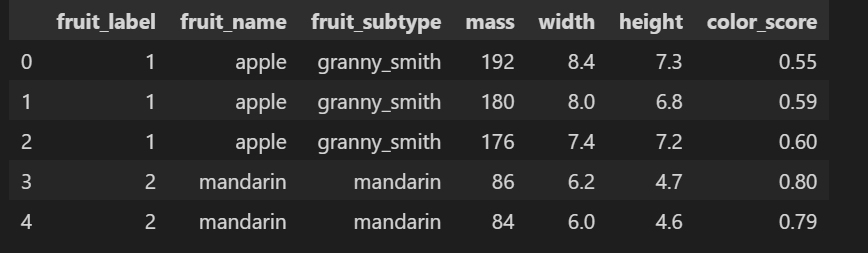
모델이 얼마나 잘 학습하고 있나 확인을 위해 정답을 갖고 있는 데이타를 활용하여 결과를 비교하자. 질량, 크기(가로,세로), 색상으로 구성된 4개의 속성으로 ['apple' 'mandarin' 'orange' 'lemon'] 4 종류의 데이타 있다.

모델 학습 방법과, k개의 어떻게 찾는지 확인해 보자..

사용된 데이타. .mass, width, height, color만 featur로 사용한다.

1) 모델 학습과 예측

지도학습과 동일하게,, 전처리.모델학습, 예측을 진행한다.

그러나 정답이 없으므로 학습할때 학습데이타만 전달하고, 평가가 없다.

from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans

from sklearn.preprocessing import MinMaxScaler


X_fruits = fruits[['mass','width','height', 'color_score']].values
y_fruits = fruits[['fruit_label']] - 1

X_fruits_normalized = MinMaxScaler().fit(X_fruits).transform(X_fruits)  

kmeans = KMeans(n_clusters = 4, random_state = 0)
kmeans.fit(X_fruits_normalized)
print(f" 0번째 데이타의 예측 확인 : { kmeans.predict(X_fruits_normalized[0:1])}")

plot_labelled_scatter(X_fruits_normalized, kmeans.labels_, 
                      ['Cluster 1', 'Cluster 2', 'Cluster 3', 'Cluster 4'])

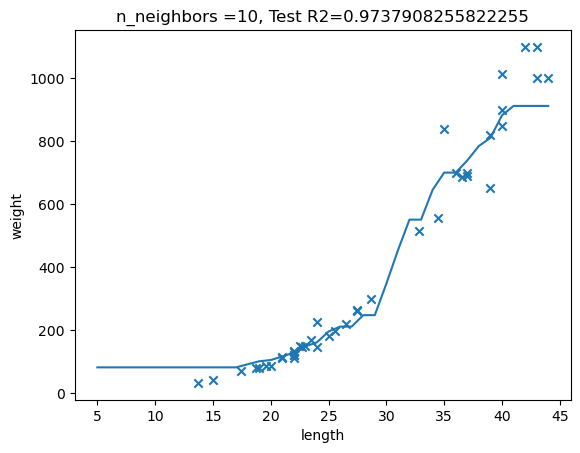
그래프는 첫번째, 두번째 feature를 이용하여 클러스터 결과를 보여준다. 가운데 부분에서 논란이 예상이 된다.

우리가 갖고 있는 정답과 모델이 예측한 값을 비교하니 다른 부분이 존재한다.

정답 label           : [[0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 2 2 2 2 2 2 2 2 2 2
  2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3]]
k-means model label : [0 0 0 1 1 1 1 1 3 3 3 3 3 0 0 0 0 0 3 3 3 3 3 3 2 2 2 0 1 3 3 3 3 0 0 0 3
 3 3 1 3 3 3 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 1]

2) 최적의 k 값 찾기

4개로 분류된다는 지식으로 k=4를 사용하였다. 지식이 없다면, 적당한 k를 찾아야 한다.  엘보우 방법은 대표적인 갯수를 찾는 방식이다.

이너셔(inertia)는 클러스터 샘플이 얼마나 가까운지를 나타낸다. 클러스터의 중심과 샘플사이의 거리의 제곱 합이다.

클러스터 개수가 늘어나면 클러스터 개개의 크기는 줄어들기 때문에 이너셔도 줄어든다.  엘보우 방법은 클러스터 개수를 늘려가면서 이너셔의 변화를 관찰한다.

즉, 클러스터 개수를 증가시키면서 이너지를 그래프로 그리면 감소하는 속도가 꺽이는 지점을 선택한다. 아래 그림 처럼 꺽이는 부분이 4이고, 이를 선택한다.

inertia = []
for k in range(2, 7):
    km = KMeans(n_clusters=k, random_state=42)
    km.fit(X_fruits_normalized)
    inertia.append(km.inertia_)

plt.plot(range(2, 7), inertia)
plt.xlabel('k')
plt.ylabel('inertia')
plt.show()

3) 실습파일

PCA 

PCA는  고차원의 데이터를 낮은 차원의 데이터로 바꿔줄 수 있다는 것인데, 중요한 것은 "어떻게 차원을 잘 낮추느냐" 이다. 즉, 10개의 컬럼의 데이타를 4개 또는 5개만 이용 할 수 있다.

(PCA는 선형대수를 좀 공부한 후에 정리를 해야겠네요...라이브러리만 쓰면 뭐 별게 아닌데... 왜 그럴까까지 따져 들어가려니..... 결국에 수학...... 고등수학에 머신러닝때문에 선형대수가 교과에 들어갔다고 하는데.. 긍정적이면서 불쌍해 보이기도하고...)

가령 우리에게는 아래와 같은 2차원 공간에 데이터들이 있다.
우리의 목표는 이 2차원 공간의 데이터를 1차원 공간의 데이터로 만들어 주는 것이다.
⇒ 차원 축소의 기본적인 컨셉. 여기에서 우리가 할수 있는 방법은 2가지 인데,

방법1 에서는 차원 x1, x2 에 냅다 데이터를 내려버렸다. 이렇게 할 경우 문제점은 내린 후에 값이 겹치는 데이터들이 많고, 아예 한 차원의 정보는 유실되게 된다.
반면 방법2 에서는 새로운 차원 (화살표) 에 데이터들을 내려줬다. 이렇게 한 결과 데이터들은 방법1에서의 문제를 어느정도 해결하게 된다.
여기서 중요한 것은 데이터들이 겹치지 않게 끔하는 화살표를 찾는 것!!!!

좌측에 사진처럼 2차원 상에서 무수히 다양한 화살표를 그릴 수 있다.
하지만 우리는 그 중 파란색 화살표 처럼 데이터를 해당 화살표에 1차원 으로 내렸을 때 겹치지 않게 하는 화살표를 찾아야 한다. (longest distance)
⇒ 정리하자면,

1. 수많은 화살표 들 중, 데이터 들을 화살표에 내렸을 때, 데이터가 최대한 안 겹치게, 멀리 퍼지게 하는 길이가 긴 화살표 찾기
2. 거기에 데이터들을 투영
3. (2차원 이상의 경우 2차원으로 만들고자 한다면)
   만약 또 하나의 화살표 만들 때 축 끼리는 직각이 되어야 함, 최대한 데이터가 겹치지 않도록

이를 선형대수학의 관점에서 해석하자면,

1. 공분산 행렬에서 고유 벡터/고유값을 구하고
2. 가장 분산이 큰 방향을 가진 고유벡터(e1) 에 입력데이터를 선형변환
3. 고유벡터(e1) 과 직교하며, e1 다음으로 분산이 큰 e2 고유벡터에 또 선형변환.

1에서 행렬 A의 공분산 행렬의 고유벡터가 데이터가 최대한 안 겹치게, 멀리 퍼지게 하는 길이가 긴 축의 벡터가 된다.(나중에 증명)
2에서 고유값이 가장 큰 것에 매핑되는 고유 벡터(e1)가 1의 고유 벡터 중 데이터의 분산이 가장 큰(데이터가 최대한 안 겹치게, 멀리 퍼지게 하는 길이가 긴) 축의 벡터가 된다.
3에서 2의 벡터와 직교하며 다음으로 고유값이 큰(다음으로 분산이 큰) 벡터(e2)를 찾는다.

PCA에 대해 깔끔하게 정리된 글... 필요성.. 원리는 어떠한지.. (결국 선형대수 T.T)

• https://velog.io/@lighthouse97/PCAPrincipal-Component-Analysis

iris를 구분하기 위해서 4개의 컬럼을 2개의 컬럼을 이용해서 분석한다.   분산량이 작은 2개 컬럼을 제거하는 예제가 좋군

• https://velog.io/@swan9405/PCA

수학적 해석(?)이 있는 자료.. 투영, 편차, covariance

• https://ddongwon.tistory.com/114

decsion tree 알고리즘이 feature를 선택하여 분류하는지 따라가다보니 모델의 cost func()까지 찾아가보게 되었군요... 

이번주 궁금한 것이 decision tree에서 분명 수식으로 계산된 값은 틀린것이 없는데 model 학습된 tree와 일치하지 않는 것이 있습니다. 소스와 데이타를 공유하니.. 무엇이 잘못되었는지 뎃글 공유해 주시면....감사하겠습니다.

(직접 계산하면 첫번째 노드가 날씨부터 분류, model의 첫번째 노드는 습도부터 분류합니다. 계산으로 유도된 노드인 날씨가 맞는것 같은데... 모델은 왜 습도를 먼저 선택했을까가 궁금합니다. 데이타 변환이 잘못된것인가 하는 의심이 듭니다만..)

One-Hot Encoding의 필요성을 느낍니다..

https://hoyokin.tistory.com/33

의사결정트리(Decision Tree)란?

• 의사결정트리는 일련의 분류 규칙을 통해 데이터를 분류, 회귀하는 지도 학습 모델 중 하나이며,
• 결과 모델이 Tree 구조를 가지고 있기 때문에 Decision Tree라는 이름을 가집니다.
• 아래 그림을 보면 더 쉽게 이해가 가능합니다.

• 위 그림은 대표적인 의사결정트리의 예시로서, 타이타닉호의 탑승객의 생존여부를 나타내고 있습니다.
• 이렇게 특정 기준(질문)에 따라 데이터를 구분하는 모델을 의사 결정 트리 모델이라고 합니다.
• 한번의 분기 때마다 변수 영역을 두 개로 구분합니다.
• 결정 트리에서 질문이나 정답은 노드(Node)라고 불립니다.
  • 맨 처음 분류 기준을 Root Node라고 하고
  • 중간 분류 기준을 Intermediate Node
  • 맨 마지막 노드를 Terminal Node 혹은 Leaf Node라고 합니다.
  • 결정 트리의 기본 아이디어는, Leaf Node가 가장 섞이지 않은 상태로 완전히 분류되는 것, 즉 복잡성(entropy)이 낮도록 만드는 것입니다.

• 주어진 문제들은 n개의 feature가 주어지고, 어떤 class에 속하는지를 decision tree model이용
• decision tree는 feature를 어떻게 tree를 만들까? Gini, Entrypy를 이용함
• GiNI 계수 확인하기 
  • length, width라는 2개의 feature로 세토사,버시컬러,버지니카 3개 class 분류 예제
  • 아래 그림은 model이 제공하는 tree임... 각 node의 gini 계수를 구할 수 있어야 함.
  • 지니 계수 $$ G_i = 1 - \sum_{k=1}^K (p_{i,k})^2  $$
  • $$ p_{i,k} $$ 는 i 번째 노드에 있는 훈련 샘플 중 클래스 k에 속한 샘플의 비율, K는 클래스의 총 개수 
  • gini = 0.168 = $$ 1 - (p_{2,세토사}) ^2 -(p_{2,버시컬러}) ^2 - (p_{2,버지니카}) ^2 $$ = $$ 1- (0/54)^2 - (49/54)^2 - (5/54)^2 $$

• 그러면 어떻게 decision tree는 분류 할까? 아래 비용함수를 최소화 하는 feature \( k \) 와  해당 특성의 임계값 \( t_k \)를 결정해서 분할하는 과정을 반복한다.
  
  • \( m, m_{left}, m_{right} \) : 각각 부모와 왼쪽, 오른쪽 자식 노드에 속한 샘플 개수
  • \( G_{left}, G_{right} \) : 각각 왼쪽, 오른쪽 사식 노드의 지니 불순도
  • $$ J(k,t_k) = \frac{m_{left}}{m}G_{left} + \frac{m_{right}}{m}G_{right} $$
  • 간단한데.. 인터넷에 돌아다니는 아래 예제를 꼬오옥 확인하자!!!
    • 지니계수로 비용함수를 최소화 하는 예제(중간쯤나이,수입,학생여부,신용등급에따른  컴퓨터구입여부)
      • https://leedakyeong.tistory.com/entry/%EC%9D%98%EC%82%AC%EA%B2%B0%EC%A0%95%EB%82%98%EB%AC%B4Decision-Tree-CART-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EC%A7%80%EB%8B%88%EA%B3%84%EC%88%98Gini-Index%EB%9E%80
    • Entryp로 node를 결정하는 예제(  중간쯤테니스  경기  참가여부)
      • https://wooono.tistory.com/104

의사결정트리(Decision Tree) - 분할 실습

• https://wooono.tistory.com/104 예제를 통해 손으로 계산 해보자!!!
• 손으로 계산을 하면 날씨부터 분류를 해야 한다. 모델로 학습을 하면 습도부터 분류를 한다... 소스코드를 제공하니 무엇이 잘못되었는지 확인부터!!

교차 검증

• 수능 시험을 보기 위해  학습하고, 모의 고사 시험을 몇 번 보고, 한번의 수능을 본다,
• 머신러닝에서도 학습 후 에 바로 시험을 볼 것이 아니라, 모의 고사를 보면 학습이 잘 될 것이다. 교차 검증은 모의 고사에 해당
• 일반화 성능이 높은 모델을 훈련시키기 위해 많이 사용되는 방식 중 하나가 교차 검증cross validation이다. 교차 검증은 훈련 데이터셋의 일부인 검증 셋validation set을 이용하여 훈련 과정중에 훈련 중인 모델의 일반화 성능을 검증하는 기법이며, 이를 통해 일반화 성능이 높은 모델을 훈련시키도록 유도한다.

• 테스트 데이터를 다르게 설정할 때마다 학습 데이터의 구성도 당연히 달라집니다. (위 그림에서 하얀색 칸 위치가 달라질 때마다 주황색 칸의 구성도 달라지고 있는게 보이죠.) 약간씩 다른 구성의 학습 데이터로 학습하는 모델이 총 k번 돌아가게 되는 셈이죠! 모델이 총 k번 돌아갔으니 결과물도 총 k개 나오게 되는 겁니다. 그리고 이 k개의 결과물들의 평균값이 K겹 교차 검증 방식을 활용한 모델의 성능이 되는 거죠!.

앙상블 

앙상블 기법 Ensemble Learning 이란 여러 개의 개별 모델을 조합하여 최적의 모델로 일반화하는 방법입니다. weak classifier 들을 결합하여 strong classifier 를 만드는 것입니다. decision tree 에서 overfitting 되는 문제를 앙상블에서는 감소시킨다는 장점이 있습니다.

대표적으로 Random Forest 모델이 있습니다.

https://medium.com/dawn-cau/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-%EC%95%99%EC%83%81%EB%B8%94-%ED%95%99%EC%8A%B5-%EC%9D%B4%EB%9E%80-cf1fcb97f9d0

이전  Decision Tree를 정리하면서 분명 수식으로 계산된 값은 틀린것이 없는데 model 학습된 tree와 일치하지 않는 것이 있습니다. 결론은 데이타를 One-Hot-Encoding해야 하는 군요.. Label Encoding을 한것이 문제였습니다.

Encoding의 필요성은  문제를 다시 정리 해보죠..

필요성을 느끼니 또 Encoding에 대해서 공부를 해야 겠군요..이건 나중에..

 1. 해결하고자 하는 문제

데이타는 아래 표와 같고, Entropy 방식으로 풀어 나가면 오른쪽 Tree와 같습니다.  Tree의 노드가 날씨부터 시작합니다.

위의 표를 데이타로 활용하면.. 아래와 같은 에러가 발생합니다.

{
"name": "ValueError",
"message": "could not convert string to float: '맑음'",

.....

}

2. Label Encoding으로 전처리 후 Decision Tree 작성의 문제

데이타를 변환해야 합니다. 날씨 컬럼의 맑음, 흐림, 비의 값을 0, 1,2 로 변환합니다. 온도, 습도, 바람 컬럼의 문자열을 적당한 숫자로 변환합니다.

입력 데이타는 아래 표와 같이 만듦니다. Decision Tree를 만들었더니, Tree의 노드가 습도부터 시작합니다.

손으로 풀어간 1)의 Tree는 날씨부터 시작하는데, 아래 트리는 습도부터 시작합니다. 맘에 안듭니다.

3. One-Hot Encoding으로 전처리 후 Decision Tree 작성

1)에서 사용된 데이타를 판다스의 get_dummies()함수를 이용하여 전처리를 합니다.사용된 코드는 아래와 같습니다.

전처리된 데이타는 아래 표와 같습니다. 날씨컬럼이 날씨_맑음, 날씨_비,날씨_흐림으로 생성이 됩니다. 이 데이타로 Decision Tree를 만들었더니 날씨로 시작하는 것을 볼 수 있습니다.

첨부 사용된 코드와 데이타

데이타와 코드를 공유 합니다.

기초 선형수학

https://angeloyeo.github.io/2019/07/27/PCA.html

tistory에서 수식 사용하기

설정 하기 : https://kosb.tistory.com/49

 수식 https://ko.wikipedia.org/wiki/%EC%9C%84%ED%82%A4%EB%B0%B1%EA%B3%BC:TeX_%EB%AC%B8%EB%B2%95

axis는 판다스의 apply(), drop(), concat()등의 많은 판다스 함수의 인자로 사용이 된다.  인자에 사용되는 0 이 행, 가로, 세로, 열에 적용되는지 헷갈린다. 한번 정리하는 시간을 갖자!!

1. 용어 정리 부터

사용되는 용어가 많이 나온다.. 근데.. 용어 정리가 안되면,  읽고 나면 또 헷갈린다. ㅋㅋ

0 = 행 = row=  가로      = 데이타

1 = 열 = column = 세로 = feature, 속성

(행렬... 수학시간에 배운 내용이 기억이 안나더라도.. 행렬은 단어는 익숙하다.

행렬에서 행이 먼저 나오므로 0, 렬=열이 나중에 나오므로 1로 기억하자..어쩔수 없다...)

2. 판다스 함수에서의 행과 열

axis=0 means along "indexes". It's a row-wise operation.

axis=0은 행, axis=1은 열이라고 무조건 외우고, 함수에 따라 2가지가 반영이 된다.

• 적용 방향을 나타난다. (.drop(),concat()등)
• 결과를 나타나는 방향이다.  (.apply(),sum() 함수등)

정도는 없는 것 같다.. axis 파라미터 사용 함수를 익힐때마다... 나름의 규칙을 생각하는 수 밖에..

2.1 적용 방향 (기본)

2.1.1 concat(axis=0)

두 테이블의 합치는 concat()는 axis=0, 1을 사용할 수 있다.

아래 예는 하나의 테이블을 기준 잡고, 다른 테이블의 행을 연결한다. 행을 적용 해야 하니... axis=0으로 설정한다.

2.2.2 drop(axis=0)

행을 삭제할때는 axis=0, 열을 삭제할때는 axis=1이다.

2.2 결과 방향

appy() 함수와 같이 axis=0을 설정하면 결과가 행으로 생성이 된다.  아래와 같이 행에 sum을 생성하기 위해서는 컬럼들의 sum을 구하게 된다.

axis=0, 결과는 행으로 생성 (행으로 생성하기 위해 컬럼들을 이용!!)

참고한 자료들

https://pandas.pydata.org/pandas-docs/stable/getting_started/intro_tutorials/index.html

https://hogni.tistory.com/49

재미있는 책들이 많이 있다는 것을 느낌..

로지스틱 회귀(이진분류, 다항분류)를 모델이 제공하는 절편과 기울기로 z 값을 구하고, sigmod(), softmax()를 이용해서 확률 값을 직접 구해 보면서 깊게 공부를 하였군요.

(softmax 정의시 np.sum() 대신 sum()을 사용하여 왜 안되나 고민하였는데.. 혼공머신에서 질문올리고 답변을 받아서 해결을 했네요... 질문을 하고 질문을 받아 줄 수 있는 환경이 좋아요 ^^)

학습한 모델이 기울기와 절편을 제대로 제공한다면 테스트 데이타를 잘 예측할 수 있을 것 같군요.  어떻게 잘 기울기와 절편을 찾을까?? 에러 코스트를 낮게 찾아야 하고 경사하강법을 사용한다...

혼공머신 4장을 참고하였습니다.

https://hongong.hanbit.co.kr/%ED%98%BC%EC%9E%90-%EA%B3%B5%EB%B6%80%ED%95%98%EB%8A%94-%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-%EB%94%A5%EB%9F%AC%EB%8B%9D/

4.1 다항 분류

• 이진분류 (0 또는 1, 1장에서처럼 빙어/도미 분류)를 학습하고 확장된  3개 이상 분류 기법을 다룬다 
• KNN, 로지스틱 회귀를 학습함.

4.2 해결할 문제

• 7종의 물고기에서 어떤 특성 (Test Data)가 주어질 떄 어떤 물고기에 속할까
• 7종의 물고기 종류 ['Bream' 'Roach' 'Whitefish' 'Parkki' 'Perch' 'Pike' 'Smelt']
• 데이타 특성은 5개이다. 
  • Weight,Length,Diagonal,Height,Width
• 데이타 샘플

4.3 KNN

• 이웃을 선택하고 (k=1,3,5) 선택된 이웃과 가까운 거리에 있는 것을 선택
• 그림은 2개의 feature로 3개의 class (원, 세모, 네모)로 분류. 책은 5개 특성, 7개 class

4.3.1 KNN 모델

KNN 모델도 일반적인 머신러닝 모델과 같이 학습,평가,예측을 한다.

85% 정확도로, Test Data 5개를 잘 분류 하였다.

Test Score : 0.85

Predict 5 Items: ['Perch' 'Smelt' 'Pike' 'Perch' 'Perch'] 

accuracy: 0.85

4.3.2 KNN 예측 결과는 어떻게 산출되었을까?

predict()은 class 값을 전달한다. predict_proba()는 class의 확률값을 전달한다.

예제 5개의 sample을 예측할 때, predict_proba()는 5개의 class에 속할 확률을 나타낸다.

predict() class에 속할 확률 속에서 높은 class를 선택한다.

첫번째 sample data(빨간색)는 Perch가 선택이 되었다. Perch의 확률은 0.66이고, Roach는 0.33이다. 높은 Perch로 선택했다.

즉, Pearch로 판정을 했지만, 100%가 아닌 66%로 확률로 판정을 했다. 모든 데이타를 100% 판정한다는 것은 가능할까? 오류를 인정해야 한다.

4.4 로지스틱 회귀

•  선형 방정식을 학습하지만, 방정식의 연속될 결과값을 분류= 카타고리=클라스로 표현한다.
• 클라스가 2개인 경우 선형 방정식의 결과 값을 sigmod() 함수를 클라스의 확률을 구하고 확률에 따라  이진 분류한다.
• 클라스가 3개 이상인 경우 각 클라스의 수 만큼 선형 방정식의 값이 계산되고, SoftMax()로 각 클라스의  
• 로지스틱은 2개 클라스(=카타고리)를 분류, SoftMax회귀는 3개 이상 클라스를 분류
• 선형 방정식을 학습하므로 연속형 값이 나오며, 이를 클라스로 매핑해야 한다.
• 로지스틱은 선형 방정식의 값(z)을 sigmod 함수와 threadhold에 따라 클라스를 구분
• SoftMax은 선형 방적식의 값(z)가 클라스 수 만큼 산출이 되고, softmax에 의해 각 클라스의 확률을 산출한다. 최종 확률이 높은 것을 선택한다.

4.4.1 로지스틱 모델 (멀티클라스)

로지스틱 모델도 일반적인 머신러닝 모델과 같이 학습,평가,예측을 한다.

실행 결과

4.4.2 로지스틱 모델(멀티클라스)은 어떻게 Test data로  예측할까?

• 학습에 의해 클래스 숫자만큼 기울기와 한개의 절편을 구한다.
• 예측데이타와 (구한)기울기로 클래스 숫자만큼 z 값을 구한다.
• (멀티class인경우) maxsoft로 각 클래스의 확률을 구한후, 확률이 가장 큰 클라스를 선택한다.
• (binaryclass인경우) sigmod로 2개의 클래스의 확률을 구한후, 확률이 가장 큰 클라스를 선택한다.

test 데이타 1개를 이용하여 기울기와 절편, SoftMax를 이용하여 클라스별 확률을 구한다.

• test 데이타는 일때
  •  [-0.88741352 -0.91804565 -1.03098914 -0.90464451 -0.80762518]
• 모델 학습에 의한 기울기와 절편으로 클라스별 z값을 구한다.
  • [-6.5   1.03  5.16 -2.73  3.34  0.33 -0.63]
• z값들에 대한 확률
  • Class 별 확률값
              Bream   Parkki  Perch   Pike    Roach   Smelt   Whitefish
    0        0.0         0.014   0.841   0.0        0.136   0.007   0.003

수행 결과

4.4.3 로지스틱 모델 (바이너리클라스)

• 데이타 분류값이 2개만 다를뿐이지 모델 학습 방법,평가, 예측은 멀티클라스와 동일하다.
• 멀티 클라스는 각각의 클라스의 z 값을 구하고, 클라스별 확률을 구했지만, 바이너리클라스는 1개(양성클라스)의 z값과 확률만 구하고 다른 1개(음성클라스는)의 확률은 1에서 뺴준다 .. (음성,양성 클라스 확률의 합계는 1이다.)
•  

실행결과

4.4.4 로지스틱 모델(바이너리클라스)은 어떻게 Test data로  예측할까?

• 실행결과를 보면 예측할 데이타로 Bream을 예측하였다. lib가 제공하는 predict_proba()의 결과는 클라스별 확률을 구하고, 높은 확률인 클라스를 선택하는 알고리즘이다.
• 음성 클라스 확률과 양성 클라스 확률의 합을 구해 보고 1이 되는 것을 확인할 수 있다.

• 모델이 학습한 기울기와 절편으로 확률을 직접 구해보자!!
  • z 값을 test 데이타 * 기울기 + 절편으로 구한다.
  • z 값을 sigmod 함수로 0~1 사이의 값을 구한다. 이 값은 양성 클라스의 확률이 된다. 음성 클라스의 확률을 1을 뺴준다.

학습한 내용

머릿속에 keyword가 없으면 다시 보기!!

미션1. 

neighbors의 수마다, Test input, test value로 R2를 계산하도록 수정

선택 미션2 - 하이퍼파라미터

• 머신 러닝이 학습할 수 없고 사람이 알려줘야 하는 파라미터
• KNN의 이웃의 수, 릿지,라소의 규제 강도인 alpha, 다중회귀에서 차원
• 모델 파라미터 vs 하이퍼 파라미터  https://towardsdatascience.com/model-parameters-and-hyperparameters-in-machine-learning-what-is-the-difference-702d30970f6
• http://dmqm.korea.ac.kr/uploads/seminar/DMQASeminar_20210924_%EB%B0%B0%ED%8F%AC%EC%9A%A9.pdf

기타 자료

- Pandas CheatSheet

https://pandas.pydata.org/Pandas_Cheat_Sheet.pdf

- Numpy CheatSheet

다운 로드 : https://images.datacamp.com/image/upload/v1676302459/Marketing/Blog/Numpy_Cheat_Sheet.pdf