1. 선형대수학에 대한 단상

좋아좋아브라이언 2024. 3. 2. 13:07

2024. 3. 2. 13:07

기본 입자는 표준 모형으로 일목 요연하게 정리된다. 이 이론의 놀라운 점은 지독하게 수학적이라는 점이다(대부분의 물리 이론이 수학적이다). 표준 모형을 통해 물리학자는 우주가 얼마나 수학적인지 다시 한번 깨닫는다.
... 하늘과 바람과 별과 인간 중에서

1. 시작하면서

머신러닝을 공부하게 되면서 행렬과 미분이 알고리즘으로 사용된다는 것을 느끼면서, 전산의 역활이 과연 무엇일까 좌절 아닌 좌절을 하고 있을 때, 나름 위안을 삼았던 문구이다..

회귀분석에 사용되는 선형 방정식도, overfitting를 방지하기 위한 L2, L1 규제, 많은 데이타를 압축하기 위한 주성분 분석 등도 선형대수학에 나오는 개념들이다. 선형 대수학이 응용되는 사례는 그림1을 보자..

혼자 공부하는 머신러닝/딥러닝을 공부하다가 나오다 마주치게 된 주성분 분석.... 목적은 차원 축소인데... 잘 이해가 안된다... 지금 보니 이해가 안되는 것이 당연하다.. 선형대수학의 마지막(??)에 나오는 이야기가 SVD 이다.. SVD를 이해하기 위해서는 소거법, 아이젠 벡터를 이해하고, 그것들이 단점을 이해해햐 하니....

그림 2는 선형대수학의 학습 순서이고, 이들의 제약사항이 기술 되어 있다. 우리의 데이타는 n*n도 아니고, 역치가 존재하지 않고, 대각행렬도 아닌 일반적인 데이타이니, SVD를 사용하게 된다... (...중간에 포기하지 마시라)

2. SVD의 응용 사례

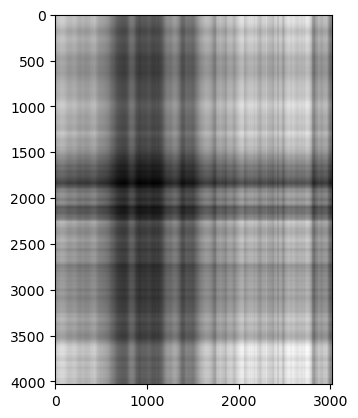
3,024* 4,032Pixe의 데이타가 아래 그림과 같이 있다고 하자..

sigular vector를 1,2,4,8,16,32,64개 추가하였을때의 변화는 아래 그림과 같다.

	n=1	n=2	n=4	n=8	n=16	n=32	n=64

sigular vector가 64개이면 원본과 비슷하게 된다.

원본 그림 (A)는 3,024* 4,032의 크기인데... SVD로 분해하면.. 64*4,032 + 64 + 64*3,024로 줄어들게 된다... 와우!!!

(SVD 보면서 정말 감탄을 하였다당..)

그 어려운 SVD 계산도 ..라이브러리를 써서 한줄로 계산한다... 두번째 와우!!!

U, sigma, V = np.linalg.svd(imgmat)

#아무이미지를 블러오고
img = Image.open('oboe-with-book.jpg')

#gray로 변환하고
imggray = img.convert('LA')

#numpy mattrix로 변환하고
imgmat = np.array(list(imggray.getdata(band=0)), float)
imgmat.shape = (imggray.size[1], imggray.size[0])
imgmat = np.matrix(imgmat)

#SVD로 분해한다.
U, sigma, V = np.linalg.svd(imgmat)

# singlua vector를 늘려준다.
for i in [2, 4, 8, 16, 32, 64]:
    reconstimg = np.matrix(U[:, :i]) * np.diag(sigma[:i]) * np.matrix(V[:i, :])
    plt.imshow(reconstimg, cmap='gray')
    title = "n = %s" % i
    plt.title(title)
    plt.show()

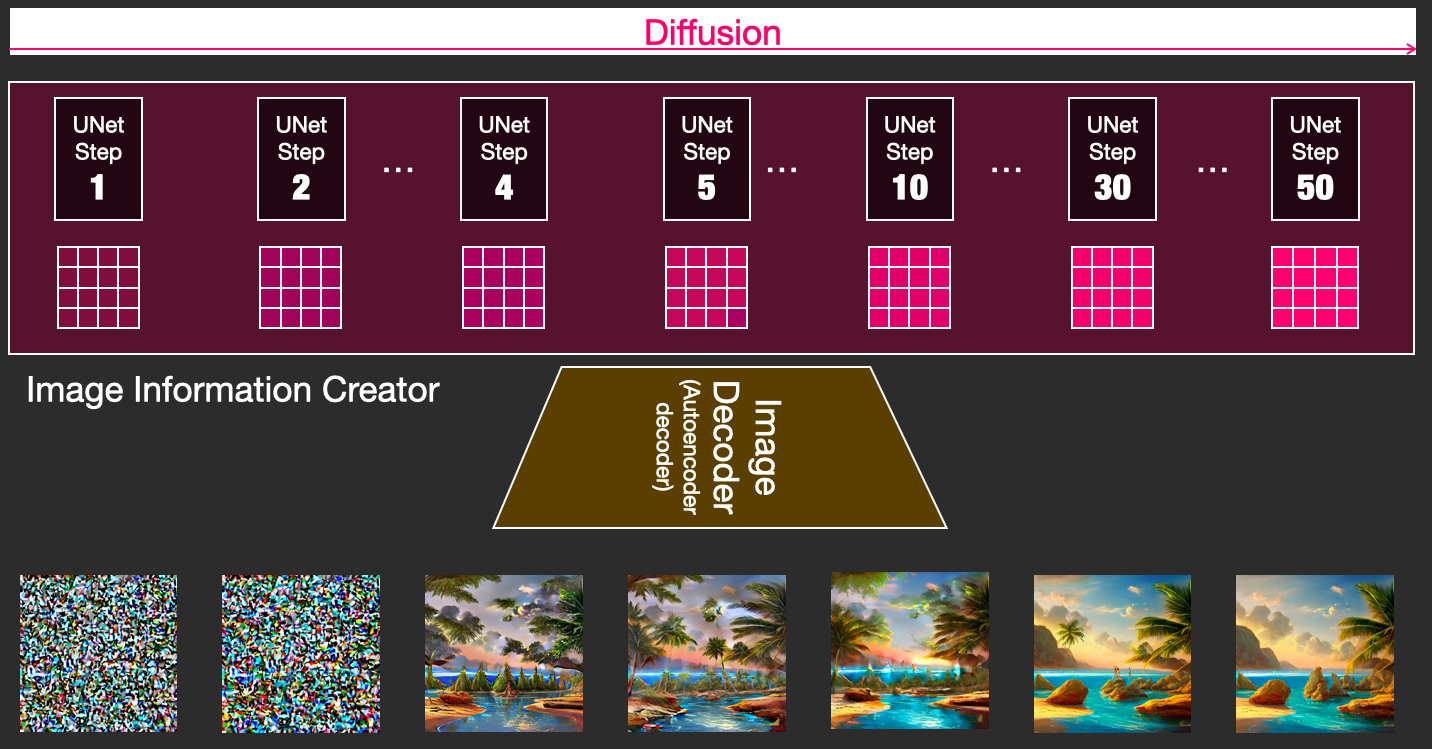
그림생성하는 Stable Diffusion의 동작 원리도 Unet Step이 증가할 때마다 최초 노이즈에서 그림으로 완성이 되는데.. Step의 증가가 single vector가 추가 되는 것이 아닐까?? 개인적인 생각임다...ㅋ

https://jalammar.github.io/illustrated-stable-diffusion/

PCA의 활용은 차원 축소라 이야기한다.. 행렬의 직관적인 의미는 음... 숫자 하나가 소인수 분해가 되어.. 인수를 찾듯이.. 행렬도 인수분해한다.. 행렬의 성격에 따라, eigen value, sigluar value라는 값으로 인수분해한다... 인수 분해 해서.. 인수를 활용한다 정도의 의미를 부여하면 되지 않을까...

(eigen ,, 독일어로 성질의 뜻.. sigular 영어의 성질의 뜻 내포..)

수학은 참으로 일반적이고 어려운 학문이다.. 나처럼 목적이 뚜렷한 사람에게 그 용도를 한정시키면 수학이 필요하구나 느끼고 재미 또한 느끼게 된다. 또한...이 어려운 것을 처음으로 활용한 선구자를 존경까지 하게 된다..